Here is a link to my video explanations to all of the mathematics questions in the 2025 ACT Online Practice Test released by ACT in January of 2025. The number of questions in the mathematics section of the enhanced ACT test online has been reduced to 45 from 60, and the number of answer choices has also been reduced to four from five. The enhanced ACT test online can be accessed at this link: Enhanced ACT Test Online.

Try the following ACT math practice question that tests your understanding of arithmetic sequences.

The first four terms of an arithmetic sequence are $a, x, b, 2x$. The ratio of $a$ to $b$ is

1. $\quad \displaystyle \frac{1}{4}$
2. $\quad \displaystyle \frac{1}{3}$
3. $\quad \displaystyle \frac{1}{2}$
4. $\quad \displaystyle \frac{2}{3}$
5. $\quad 2$

Choice B

Video Explanation

Try the following ACT math practice question that tests your understanding of mixture questions.

How many liters of a $12$ percent alcohol solution must be added to $6$ liters of a $24$ percent alcohol solution to obtain a solution that is $15$ percent alcohol?

1. $\quad 9$
2. $\quad 15$
3. $\quad 18$
4. $\quad 20$
5. $\quad 24$

Choice C

Video Explanation

Try the following ACT math practice question that tests your understanding of reflection of points across the vertical axis and straight lines in the coordinate plane.

In the $xy$-coordinate plane, point $A$ is the reflection of the point with coordinates $(4, 2)$ across the straight line $y = x$. If point $B$ is the reflection of point $A$ across the $y$-axis, what are the coordinates of point $B$?

1. $\quad (2, -4)$
2. $\quad (-2,-4)$
3. $\quad (-2, 4)$
4. $\quad (-4, -2)$
5. $\quad (-4,2)$

Choice C

Video Explanation

Try the following ACT math practice question that tests your understanding of finding areas of unusually shaped quadrilaterals.

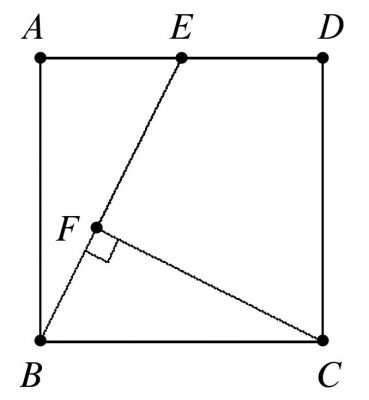
In the figure shown above, $ABCD$ is a $2 \times 2$ square, $E$ is the midpoint of $\overline{AD}$, and $F$ is on $\overline{BE}$. If $\overline{CF}$ is perpendicular to $\overline{BE}$, then the area of quadrilateral $CDEF$ is

1. $\quad 2$
2. $\quad 3-\dfrac{\sqrt{3}}{2}$
3. $\quad \dfrac{11}{5}$
4. $\quad \sqrt{5}$
5. $\quad \dfrac{9}{4}$

Choice C

Video Explanation