Finding area of a quadrilateral: ACT Math Practice Question

Try the following ACT math practice question that tests your understanding of finding areas of unusually shaped quadrilaterals.

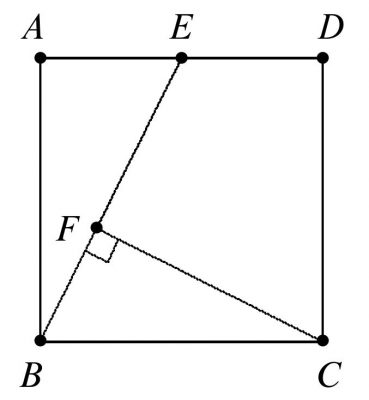
In the figure shown above, $ABCD$ is a $2 \times 2$ square, $E$ is the midpoint of $\overline{AD}$, and $F$ is on $\overline{BE}$. If $\overline{CF}$ is perpendicular to $\overline{BE}$, then the area of quadrilateral $CDEF$ is

1. $\quad 2$
2. $\quad 3-\dfrac{\sqrt{3}}{2}$
3. $\quad \dfrac{11}{5}$
4. $\quad \sqrt{5}$
5. $\quad \dfrac{9}{4}$

Choice C

Video Explanation