If you are talking about Question 60, then one could use the answer choices but it is more work than doing it directly. One still would need to recognize that the measure of angle KPM is (11x)/2 and set this to equal to different answer choices and compute the value of x. Then with that value of x, one would need to the check if (4x+18) turns out to be equal to (11x)/2.
Cumulative means the data accumulated to the number before. Meaning the second data includes12 Student’s from 65-70. So If 65-80 is 13 students then 1 has to be 71-80.
Yes, I just checked and the Reading answers are correct here. At least that is what I have in the answer official answer sheet. But I did have a wrong set on the main page where the link to this test is organized, I have fixed that one.
I have attached a screenshot from the official TIR of ACT 74F.
Can you explain 59 again? Why can’t sine theta be greater than 1 ? Do I need to know the unit circle for this? How can I use the given range of radian measures to help me solve? Thanks
Sorry for the delay. You can think of sin theta as the ratio of opposite to hypotenuse in a right triangle and this ratio is less than or equal to one. It is equal to one when the angle is 90 degrees. You can also use the unit circle approach, where sine of theta is equal to the y-coordinate of the point on the circle.
To satisfy the condition, $|\sin \theta| \geq 1$, the only way this will happen is if $\sin \theta$ is equal to $+1$ or $-1$, and these happen at $\pi/2$ and $-\pi/2$. These happen at the top and bottom of the unit circle.
There are two ways to approach this question, the first is by converting the dimensions in feet to yards and then compute the area in square yards. This would mean that the 15 feet by 21 feet rectangle is equivalent to 5 yard by 7 yard, which is equivalent to 35 square yards.
The second approach is by first calculating the area in square feet, which would be 15 times 21 or 315 square feet, in this case we have to use the conversion of 1 square yard to square feet. There are 9 square feet in one square yards, why because a 1 yard by 1 yard square is a 3 feet by 3 feet square, which has an area of 9 square feet. So to convert 315 square feet to square yards, we have to divide by 9 to find the equivalent area in square yards. I hope this makes sense.
Is there any other way to solve this?
If you are talking about Question 60, then one could use the answer choices but it is more work than doing it directly. One still would need to recognize that the measure of angle KPM is (11x)/2 and set this to equal to different answer choices and compute the value of x. Then with that value of x, one would need to the check if (4x+18) turns out to be equal to (11x)/2.
41 needs to be explained in a different way. Need to understand the concept of ‘frequency chart’ and ‘cumulative number’.
Cumulative means the data accumulated to the number before. Meaning the second data includes12 Student’s from 65-70. So If 65-80 is 13 students then 1 has to be 71-80.
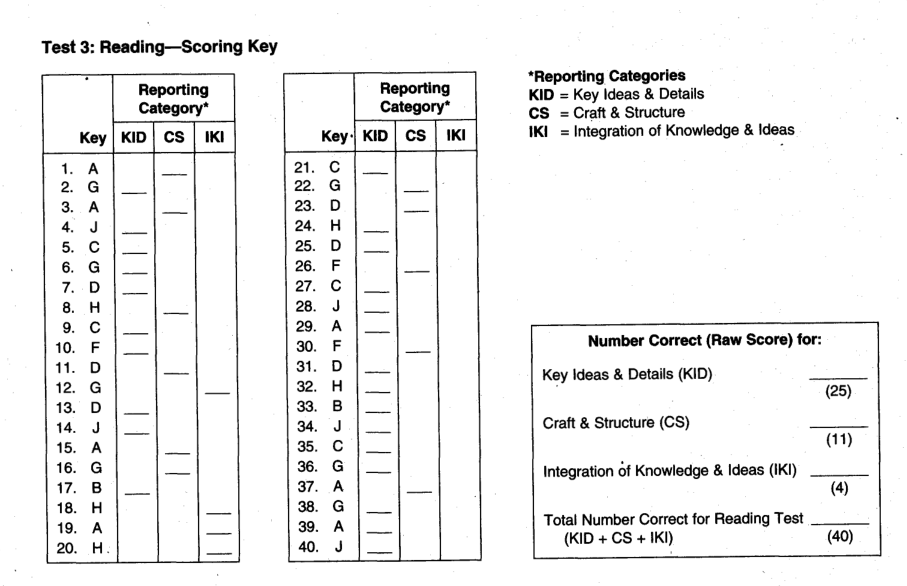
The reading answers are completely wrong
Thank you for catching the mistake. I have fixed the answer sheet.
are you sure the reading answers are fixed now?
Yes, I just checked and the Reading answers are correct here. At least that is what I have in the answer official answer sheet. But I did have a wrong set on the main page where the link to this test is organized, I have fixed that one.
I have attached a screenshot from the official TIR of ACT 74F.
Dabral
Can you explain 59 again? Why can’t sine theta be greater than 1 ? Do I need to know the unit circle for this? How can I use the given range of radian measures to help me solve? Thanks
Hi Beckie,
Sorry for the delay. You can think of sin theta as the ratio of opposite to hypotenuse in a right triangle and this ratio is less than or equal to one. It is equal to one when the angle is 90 degrees. You can also use the unit circle approach, where sine of theta is equal to the y-coordinate of the point on the circle.
To satisfy the condition, $|\sin \theta| \geq 1$, the only way this will happen is if $\sin \theta$ is equal to $+1$ or $-1$, and these happen at $\pi/2$ and $-\pi/2$. These happen at the top and bottom of the unit circle.
I hope this makes sense.
For number 47, can you please explain why it is correct to divide 15 by 3 and 21 by 3 to get 5×7, instead of diving 315 by 3 to get 105? Thank you.
Hi Quinn,
There are two ways to approach this question, the first is by converting the dimensions in feet to yards and then compute the area in square yards. This would mean that the 15 feet by 21 feet rectangle is equivalent to 5 yard by 7 yard, which is equivalent to 35 square yards.
The second approach is by first calculating the area in square feet, which would be 15 times 21 or 315 square feet, in this case we have to use the conversion of 1 square yard to square feet. There are 9 square feet in one square yards, why because a 1 yard by 1 yard square is a 3 feet by 3 feet square, which has an area of 9 square feet. So to convert 315 square feet to square yards, we have to divide by 9 to find the equivalent area in square yards. I hope this makes sense.
Dabral