Circles in the Coordinate Plane: Key Concepts
- A circle in a coordinate plane is the set of all points that are equidistant from a given point, called the center of the circle. The figure below shows a circle with the center located at $(h, k)$.
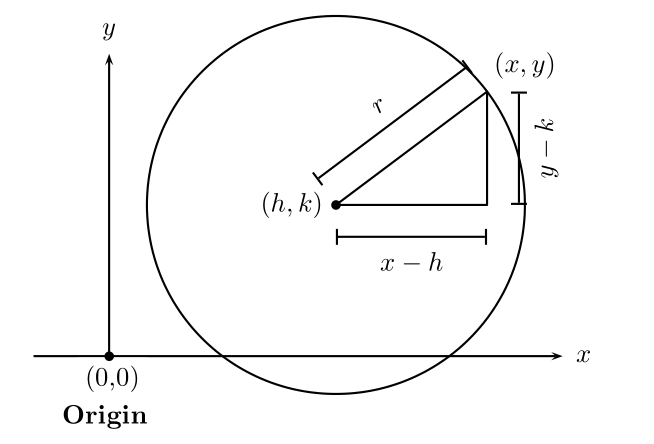
If $(x, y)$ is any point on the circle, then the distance between the
point $(x, y)$ and the center of the circle $(h, k)$ is a constant and is equal to the radius of the circle. The application of Pythagorean theorem to the right triangle shown inside the circle yields:
$$ (x-h)^2 + (y-k)^2 = r^2 $$
This is called the standard form for the equation of the circle. Once we write the equation of a circle in the standard form, we can easily find out the center and the radius of the circle.
- If the circle is centered at the origin $(h, k) = (0,0)$, then the equation of the circle simplifies to $x^2 + y^2 = r^2$.
- Expanded form of an equation of a circle: If we start with the following equation of a circle
$$(x-3)^2 + (y+2)^2 = 4^2$$
which has a center at $(3, -2)$ and a radius of 4, and expand and combine all the like terms we obtain:
$$ x^2 – 6x + 9 + y^2 + 4y + 4 = 16$$
$$x^2 + y^2 -6x + 4y=3$$
This final equation is called the expanded form of the equation of the circle.
- Expanded form to Standard form: On the ACT, you will often be given the equation of a circle in the expanded form and and you will be asked to find the center and the radius of the circle. To do that we will need to go in reverse by completing the squares in the following steps:
$$x^2 + y^2 -6x + 4y=12$$
$$x^2 – 6x + y^2 + 4y = 12$$
$$(x-3)^2 – 9 + (y+2)^2 – 4 = 12$$
$$(x-3)^2 + (y+2)^2 = 25 = 5^2$$
The circle above is centered at $(3, -2)$ and has a radius of $5$ units.

If $(x, y)$ is any point on the circle, then the distance between the
point $(x, y)$ and the center of the circle $(h, k)$ is a constant and is equal to the radius of the circle. The application of Pythagorean theorem to the right triangle shown inside the circle yields:
$$ (x-h)^2 + (y-k)^2 = r^2 $$
This is called the standard form for the equation of the circle. Once we write the equation of a circle in the standard form, we can easily find out the center and the radius of the circle.
$$(x-3)^2 + (y+2)^2 = 4^2$$
which has a center at $(3, -2)$ and a radius of 4, and expand and combine all the like terms we obtain:
$$ x^2 – 6x + 9 + y^2 + 4y + 4 = 16$$
$$x^2 + y^2 -6x + 4y=3$$
This final equation is called the expanded form of the equation of the circle.
$$x^2 + y^2 -6x + 4y=12$$
$$x^2 – 6x + y^2 + 4y = 12$$
$$(x-3)^2 – 9 + (y+2)^2 – 4 = 12$$
$$(x-3)^2 + (y+2)^2 = 25 = 5^2$$
The circle above is centered at $(3, -2)$ and has a radius of $5$ units.
Leave a Reply